本文章包含以下章节内容:
真空中的恒定磁场
磁介质
真空中的恒定磁场
恒定电流
电流定义式
I = \frac{dq}{dt}
电流密度
\vec{j} = \frac{dI}{dS}\vec{e_n}
dI = \vec{j}\cdot d\vec{S}
电流连续性方程
\oiint_S \vec{j}\cdot d\vec{S} = \oiint_S dI = -\frac{d\vec Q}{dt}
注意这个负号!
负号代表由内向外
S为导体内任意封闭平面
特别地,当 \frac{dQ}{dt} =0 ,为恒定电流。
欧姆定律
I = \frac{U}{R} = \frac{V_1-V_2}{R}
其中
R = \rho\cdot\frac{l}{S}
\rho 为电阻率。
电导率 \sigma = \frac{1}{\rho},单位为 \Omega^{-1}\cdot m^{-1} 。
欧姆定律微分形式:
\vec{j} = \sigma\vec{E}
电动势
\epsilon = \int^+_- \vec{F_{Ek}} \cdot d\vec{l}
负到正:内部
由于电源外没有非静电力做功,因此沿回路一圈非静电力做功也等于电动势,公式留作习题。
磁场 磁感应强度
洛伦兹力
\vec{F} = q\vec{v}\times\vec{B}
叉乘方向:符合右手螺旋定律
[重点] 毕奥─萨伐尔定律(B-S定律)
原始形式
直接写矢量形式:
d\vec{B} = \frac{\mu_0}{4\pi} \frac{Id\vec l\times\vec{e_r}}{r^2}
描述了电生磁
曲线积分形式省略,感兴趣的话可以自己写一下,此外这个不算是真正的积分,应该算叠加。
实际操作中一般是换元后可以直接求出 Id\vec l\times\vec{e_r} 的微分值,然后用另一个参数去算积分。
二级结论
载流直导线的磁场
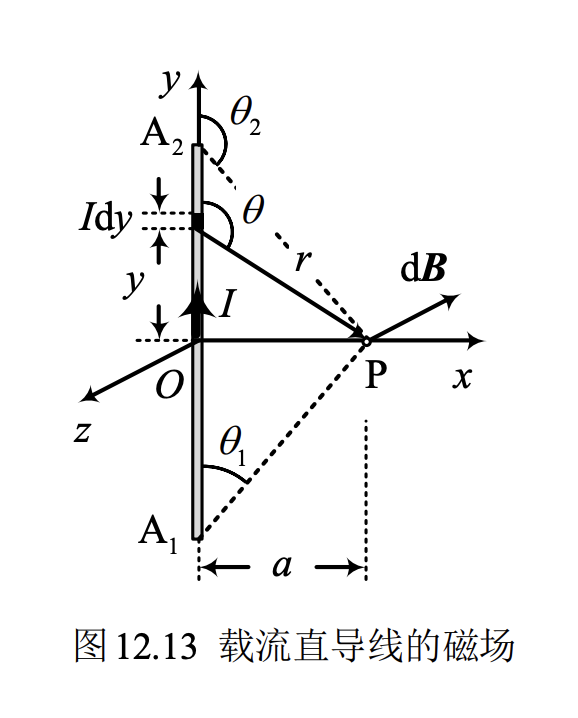
B = \frac{\mu_0I}{4\pi a}(cos\theta_1-cos\theta_2)
其中 \theta_1 \theta_2 按顺序为电流正方向与P点的夹角。
令 \theta_1 = 0 \theta_2 = \pi 易证无限长载流直导线磁场:
B = \frac{\mu_0I}{2\pi a}
圆电流轴线上任意一点的磁场
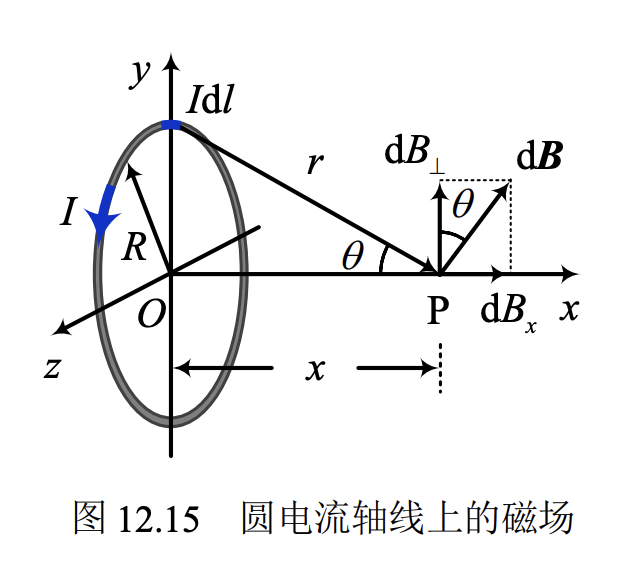
中心点有:
B_0=\frac{\mu_0I}{2R}
轴线上其他位置有:
B = B_0sin^3\theta
磁矩
\vec{m} = NIS\vec{e_n}
方向与电流方向符合右手螺旋定则
磁矩改写后的公式比较难记,应该也用不上,这里省略。
直螺线管轴线上的磁场
要求 l>>R 。
内部:
B=\mu_0nI
两端:
B=\frac12\mu_0nI
其中 n 为单位长度内的匝数。
真空中恒定磁场的基本定理
磁感应线——省略
磁通量
单位:Wb
\Phi = \vec{B}\cdot\vec{S}
同样微分形式有:
d\Phi = \vec{B}\cdot d\vec{S}
计算曲面的磁通量求个二重积分就行,在此不过多赘述。
真空磁场的高斯定理
封闭曲面磁通量为0
[重点]真空磁场的安培环路定理
\oint_L\vec{B}\cdot d\vec{l} = \mu_0\sum I_i
或者对于电流连续分布的载流体:
\oint_L\vec{B}\cdot d\vec{l} = \mu_0\iint_S\vec{j}\cdot d\vec{S}
其中S是以闭合回路L为边界的任意曲面
可用于证明无限长的载流直导线磁场、直螺线管中的磁场
磁场对电流的作用
安培定律
d\vec{F} = Id\vec{l}\times\vec{B}
均匀磁场对线圈的作用
M = \vec{m} \times \vec{B}
磁场力与磁力矩的功
A =NI\Delta\Phi

